Defining your datamodel

Imaging you got three entity types

• part-orders
• orders
• types

where each part-order instance must belong to order instance. In addition each part-order must reference a type instance as well well. Beside that the keys of the instances of all the entity types must be unique.

The subsequently picture points out those relations.

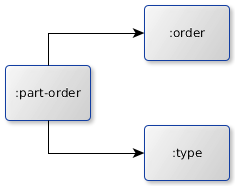
Creating the context from the metamodel

(ns lambdaroyal.memory.core.test-context
  (require [lambdaroyal.memory.core.context :refer :all]))

(def meta-model
  {:type
   {:unique true :indexes []}
   :order
   {:unique true :indexes []}
   :part-order
   {:unique true :indexes [] :foreign-key-constraints [
                                                       {:name :type :foreign-coll :type :foreign-key :type}
                                                       {:name :order :foreign-coll :order :foreign-key :order}]}})

(def ctx (create-context meta-model))

So just ordinary clojure sequence types. The relations between the entity types are modeled as referential integrity constraints here denoted by :foreign-key-constraints

Adding Reference Integrity Constraints (RIC) at runtime

Having two collections without reference integrity constraints from the very beginning is no problem. One could add a constraints from collection :order to collection :type by the following snippet

(add-ric ctx {:name :order->type :coll :order :foreign-coll :type :foreign-key :type})

where :name within the passed-in map is optional

Creating a transaction

Here a transaction is just a small wrapper around the context. All user-scope functions for inserting, selecting and updating documents require this transaction to be scoped.

(def tx (create-tx ctx))

Inserting a document into the database

Lets insert a type, a order and two part-orders into our database.

(dosync
  (insert tx :type 1 {:name :gotcha})
  (insert tx :order 1 {:name "my-first-order"})
  (insert tx :part-order 1 {:type 1 :order 1 :what-do-i-want :speed})
  (insert tx :part-order 2 {:type 1 :order 1 :what-do-i-want :grace}))

Selecting one element by key

Get back the most recently added part-order

(def x
  (dosync
    (select-first tx :part-order 2)))

Updating a document

Lets update the second part-order to have some additional data as well as an updated attribute

(dosync
  (alter-document tx :part-order x assoc :what-do-i-want :lipstick :how :superfast))

Selecting documents

There a two ways to retrieve documents from the database; by key and by indexed attribute sets. Either way one has to define a range over the the document keys or the value of an indexed attribute set by providing a start-condition and optionally a stop-condition. A condition is given by a comparative operator and an operand.

Selecting by key

(dosync
  (select tx :part-order >= 0 < 2))

Turns out to return the first part-order instance, since the second one with key = 2 fails to match the key range 0 <= x < 2.

(dosync
  (select tx :part-order >= 0))

This just returns all part-order instances.

Selecting by indexed attribute set

Indexed are defined over tuples of entity type attributes. One can manually decorate the metamodel with index definitions. When having referential integrity constraints like in our example datamodel, then you get respective indexes for free. Let's use them

(dosync
  (select tx :part-order [:type] >= [1]))

This returns all part-order instances that refer the type instance with key 1 in logarithmic time with respect to the number of part-orders stored in the db. The oddy wrapping of the :type keyword into a vector is due to the fact that indexes are defined on attribute sets rather than one single attributes.

So one could have the following meta-model that denotes an index on the order entity type that speeds up selects when searching ether via attribute set [:client :number] or via attribute set [:client]

(def meta-model
  {:type
   {:unique true :indexes []}
   :order
   {:unique true :indexes [{:name :client-number :unique false :attributes [:client :number]]}
   :part-order
   {:unique true :indexes [] :foreign-key-constraints [
                                                       {:name :type :foreign-coll :type :foreign-key :type}
                                                       {:name :order :foreign-coll :order :foreign-key :order}]}})

Select using this indexed attribute set to get all order documents that have :client = 1 and :number in range [2 3]

(dosync
  (select tx :order [:client :number] >= [1 2] < [1 4]))

Deleting a document

Lets clean up a bit

(dosync
  (delete tx :part-order 2))

Search Abstractions

Refer to namespace

lambdaroyal.memory.abstraction.search

Search abstractions help you to get projections of your data, performing many queries in parallel whose results are combined together and to handle real-world aspects like query timeout with little amount of codes.

Search abstractions make heavy use of clojure.core/async that bring asynchronous programming using channels to the stake. This allows easy and efficent creation of thousands of parallel activity streams without getting trapped by thousands of I/O consuming threads.

Search Abstractions for doing queries in parallel

Just imagin' you could start 10 concurrent queries, handling timeout and combining those results that fetched-in before the timeout occured. If you think that's a real-world use case, then go on reading.

First building block is the function

(defn abstract-search [λ] ...)

This higher order function takes a function λ into account that produces a lazy sequence as a search result and returns a function λ' that in turn returns a channel where the result of function λ is pushed to.

example would be a function that returns all tuples from a collection, we turns this into a channeled version

(defn search-coll [ctx coll-name & opts]
  (abstract-search 
   (fn []
     (let [tx (create-tx ctx)]
       (select tx coll-name)))))

Second building block is an aggregator function that combines the result of the individual queries created using the above abstract-search. A aggregator function takes one argument [n], where n is a result from one of the individual queries.

We have several standard aggregators in place

The *concat-aggregator assumes a vector STM ref to exist where all the query results are concatenated to, bear in mind that the final result might contain the same tuple more than once.

(defn concat-aggregator [ref data] ...)

The set-aggregator combines results into a set, given by STM ref. This eliminates doubles from the result.

(defn set-aggregator [ref data] ...)

Using a sorted-set-by eliminates doubles as well and combines the result into a sorted map given by STM ref. Sorting is done based on the comparator used to create the sorted set, so this is out of the equation here and due to the user of the function. But we offer a default implementation that is provided by the function

gen-sorted-set

BUT precondition for this to behave as expected is that a query returns user scope tupels where :coll is a key within the second value and its value denotes the collection this tuple belongs to. Valid example would be

[123 {:name "foo" :coll :great-foos}]

Now we have all thing in place to perform combined searches using

(defn [combined-search fns agr query & opts] ...)

where

• fns is a sequence of query functions, each a result of applying abstract-search
• agr the aggregator function
• query a parameter passed to each query function fn of fns, this might be a vector or some other non-atomic data
• opts options, see below

The following options are accepted

• :timeout value in ms after which the aggregator channel is closed, no more search results are considered.
• :minority-report number of search function fn in [fns] that need to result in order to close the aggregator channel is closed and no more search results are considered.
• :finish-callback a function with no params that gets called when the aggregator go block stops.

Let's get our hands dirty and use this to start the action.

Here we combine all the tuples from collections :a, :b and :c using the set-aggregator and print the number of elements after all queries returned.

(let [result (atom #{})]
  (combined-search [(search-coll ctx :a)
                    (search-coll ctx :b)
                    (search-coll ctx :c)]
                     (partial set-aggregator result) 
                     nil 
                     :finish-callback (fn [] (-> @result count println))))

Now the version that suffices with the result of two queries out of three

(let [result (ref #{})]
  (combined-search [(search-coll ctx :a)
                    (search-coll ctx :b)
                    (search-coll ctx :c)]
                     (partial set-aggregator result) 
                     nil
                     :minority-report 0 
                     :finish-callback (fn [] (-> @result count println))))

A note about performance - the concat-aggregator, less convenient, is considerably faster than the set-aggregator. Aggregating 60000 elements (30000 unique elements) with the concat-aggregator on an ordinary vector STM takes two magnitudes less time than by using the set operator that has to calculated hashes on quite large documents.

Refer to ns lambdaroyal.memory.abstraction.test-search-abstraction for details

concat aggregation took (ms)  4
set concat aggregation took (ms)  506

So if you know that queries do result in disjunct data and you can cope with the sorting provided by the queries itself, stick to the lightning fast concat-aggregator.

And finally the version that suffices with two queries out three or a timeout of a second

(let [result (ref #{})]
  (combined-search [(search-coll ctx :a)
                    (search-coll ctx :b)
                    (search-coll ctx :c)]
                     (partial set-aggregator result) 
                     nil
                     :minority-report 0 
                     :timeout 1000
                     :finish-callback (fn [] (-> @result count println))))

Search for getting projections on your data

Lets assume you got the following metamodel, so your :partorder tupels refer both an :order tupel as well as a :type tupel, where as each :order tupel associates a :client tupel.

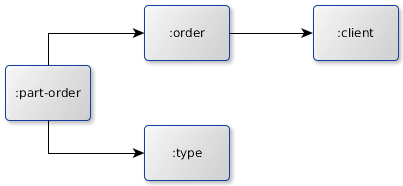
This relationship modell is implemented by the following metamodel

(def meta-model
  {:client {:indexes []} 
   :type {:indexes []}
   :order {:indexes []
           :foreign-key-constraints [{:foreign-coll :client :foreign-key :type}]}
   :part-order {:indexes [] 
                :foreign-key-constraints [{:name :type :foreign-coll :type :foreign-key :type}
                                          {:name :order :foreign-coll :order :foreign-key :order}]}})

Core of the projection is the higher order function proj

(defn proj [tx λ & path-fns] ...)

which takes a higher order functions λ into account that that returns a function whose application results in a seq of user scope tupels AND metadata with :coll-name denoting the collection the tupels belong to. Furthermore this function takes a variable number of path functions [path-fns] into account. The first one is supposed to take the outcome of application of λ into account, all others are supposes to take the outcome of the respective predessor path-fn into account. All are supposed to produce a seq of user scope tupels that is consumable be the respective successor path-fn AND metadata denoting the collection name by key :coll-name.

We take a shortcut here and give a full-fletched example with respect to our meta model that returns all :part-order tupel that refer to order which in turn refer to a :client tupel with key 2.

(proj tx
      (filter-key tx :client 2)
      (>>> :order)
      (>>> :part-order))

filter-key is one of the grazy λs that return a function itself, which applied result in a set of user scope tupels with the meta data necessary for the combination with the path functions (here >>>).

One could easily write a custom super-duper λ or one cound just stick to those we provide:

(defn filter-all [tx coll-name] ...)

A higher order function that returns a function that returns a sequence of all tuples within the collection with name [coll-name].

(defn filter-key [tx coll-name key] ...) (defn filter-key [tx coll-name start-test start-key] ...) (defn filter-key [tx coll-name start-test start-key stop-test stop-key])

Higher order functions that returns a function that returns a sequence of all tupels whose key is equal to [key], or matches the constraints provided, start-test and stop-test are just boolean functions.

(defn filter-index [tx coll-name attr start-test start-key]) (defn filter-index [tx coll-name attr start-test start-key stop-test stop-key])

Higher order functions that return a function that returns a sequence of all tupels that are resolved using a index lookup using the attribute seq [attr] and the comparator [start-test] as well as the attribute value sequence [start-key]. The second version 'lambdas' the index search for a range additionally taking [stop-test] and [stop-key] into account.

In addition to the filter function we need functions that join the associated collection. So we can climb the collection tree up to the desired collection we are actually interested in. Furthermore these function can optionally take a filter function into account that decides what associated collection tuples are to be considered.

We provide two default implementations, the first takes an additional filter into account, the later one does not restrict the result.

(defn >> [target filter-fn & opts] ...) (defn >>> [target & opts] ...)

Here opts can contain

• :ratio-full-scan iff greater or equal to the ratio (count keys / number of tuples in target of [0..1]) then the source collection is fully scanned for matching tuples rather than queried by index lookups. If not given, 0.4 is the default barrier.
• :parallel iff true (default) then all the index lookups as per individual input user tupels are performed concurrently
• :verbose iff true then one get statistics information on projection internals like full-scan vs. recurring index seeks as well as size of the target collection
• :foreign-key iff given and multiple RICs associate collection a to collection b, then this key uniquely denotes the RIC to take into account for the projection

Getting Data Hierarchies

Background

Building hierarchies groups data recursivly as per a set of discriminator functions. The leaves of the hierarchie tree are mapped using a mapper-fn.

Namespace

lambdaroyal.memory.abstraction.search

functions

(defn hierarchie "[level] is variable arity set of keywords or function taking a document into account and providing back a category. [handler] is a function applied to the leafs of the hierarchie. Using identity as function will result the documents as leafs." [xs handler & levels] ...)

(defn hierarchie-ext "builds up a hierarchie where a node is given by it's key (level discriminator), a map containing extra info that are characteristic for (an arbitrary) document that fits into this hierarchie as well as all the matching documents classified by the values of the next category (if any) or the matching documents as subnodes. [level] is variable arity set of taking a document into account and providing back a tuple [category ext], where category is a keyword or function providing back the category of a document whereas ext is a keyword or function providing back the the characteristics of a document with respect to the category. [handler] is a function applied to the leafs of the hierarchie. Using identity as function will result the documents as leafs." [xs handler & levels] ...)

The later one does consume for each group a function ext that is applied to the first element of the group in order to give back a categorie that is conj to the group key [level-val count category], where level-val denotes the result of applying the level discrimator function, count the number of elements WITHIN the next recursion matching the category and category the result of applying the category function ext to the first element matching the group.

Example

Consider the following input data

(def xs [{:color :red :shape :teardrop :count 1} {:color :red :shape :cube :count 2} {:color blue :count 10}]

can used to create a hierachie by

(hierarchie xs :count [:color :shape])

and results to

([[:red 2][[[:teardrop 1]1] [[:cube][1]]][[:blue 1]10]])

Backtracking Providing aggregated data bottom-up

(hierarchie-backtracking xs handler backtracking-fn & levels)

where backtracking-fn must accept boolean [leaf] denoting whether we operating on the outcome of leaf processing, the group key k, and a sequence of elements that result from applying a level discriminator to xs. k is [level-val count], where level-val denotes the result of applying the level discrimator function, count the number of elements WITHIN the next recursion matching the category. The function must return a adapted version of k that reflects the information necessary to the user.

Example of the application

(let [data [{:size :big :color :red :length 1} {:size :big :color :green :length 2}{:size :big :color :green :length 3} {:size :huge :length 100}]]
    (hierarchie-backtracking data identity
                                   (fn [leaf k xs]
                                     (do
                                       ;;(println :leaf leaf :k k :xs xs)
                                       (if leaf 
                                         (conj k (apply + (map :length xs)))
                                         (conj k (apply + (map #(-> % first last)))))
                                       )) 
                                   :size :color))

results in

'([[:big 3 6] ([[:red 1 1] [{:color :red, :length 1, :size :big}]] [[:green 2 5] [{:color :green, :length 2, :size :big} {:color :green, :length 3, :size :big}]])] [[:huge 1 100] [{:length 100, :size :huge}]])))